生化学 SEIKAGAKU
Journal of Japanese Biochemical Society

はじめに，ミカエリス・メンテンの式に従う酵素反応のデータの特徴を復習したい．ミカエリス・メンテンの式は式1で表される．$$\begin{array}{}\text{(1)}& v=\frac{V_{\max }\left[\text{S}\right]}{K_{\text{M}}+\left[\text{S}\right]}\end{array}$$この式でv，V_max，K_Mは，それぞれ，初速度，最大速度，ミカエリス定数である．二基質以上の酵素反応の場合は，注目している基質（S）以外の基質の濃度は一定にするので，それらの濃度はV_max，K_Mの中に含まれる．

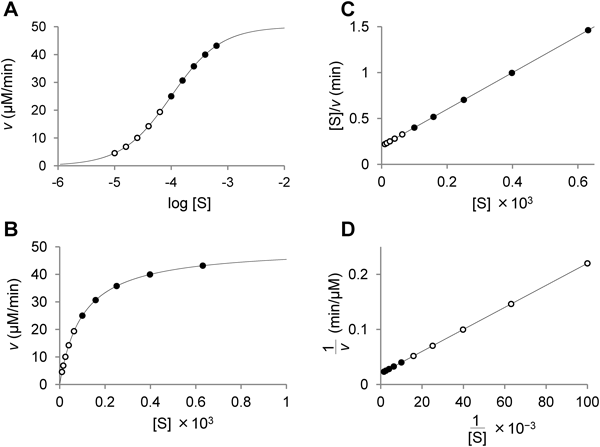
さて，基質濃度をどの程度の範囲で変えて実験すべきか．酵素の専門書¹⁾には，少なくともK_M値の10分の1から10倍の濃度範囲でまんべんなく初速度を測定することが推奨されている．その理由は，初速度を基質濃度の常用対数に対してプロットした図（図1A）をみるとよくわかる．図には，仮想的な10個のデータポイントを，K_M値未満の基質濃度のデータを白丸，K_M値以上の基質濃度のデータを黒丸で区別して，理論曲線上に示した．初速度と基質濃度の関係の全体像が，これらすべてのデータポイントをつなぎあわせることでようやく明らかになる．

図1 初速度と基質濃度の関係のいろいろな表示法

理論曲線とデータポイントは，K_M=1.0×10⁻⁴ M，V_max=50 µM/minを用いてミカエリス・メンテンの式1に基づいて計算した．

初速度を基質濃度に対してプロットして同じデータを図示すると（図1B），K_M値未満の基質濃度のデータが曲線の初めの部分にかなり密集する．次に，よく利用される直線プロットではどうなるだろうか．基質濃度と初速度の比（[S]/v）を基質濃度に対してプロット（Hanes–Woolfプロット，図1C）すると，直線のほとんどの部分をK_M値以上の濃度のデータが占めるのがわかる．一方，古くから汎用される二重逆数プロット（double–reciprocalプロット，Lineweaver–Burkプロット，図1D）では，直線のほとんどをK_M値未満の濃度のデータが占める．

二重逆数プロットでデータポイントが五つ程度の図をよく見かけるが，それでは情報不足の可能性が高い．また，ミカエリス・メンテンの式1に従わないので，二重逆数プロットで直線になる部分だけを使ってV_maxとK_Mの値を求めましたとテキストに述べ，これらの数値だけが表にまとめられていることも多い．有意義なkineticsの実験をするには，横軸を基質濃度の常用対数にとってデータをみること，そこに生理的な基質濃度範囲を重ねること（図2参照）が大切だと思う．信頼するに足る生データを共有してこそ，反応機構や生理的意義を議論することができる．

図2 フラビン酵素の基質活性化と阻害

（A）筆者らの未発表データ．（B）文献12のデータを式E2で再解析．（C）文献14のデータをE2で再解析．両矢印は生理的な基質濃度の変動範囲を示す．

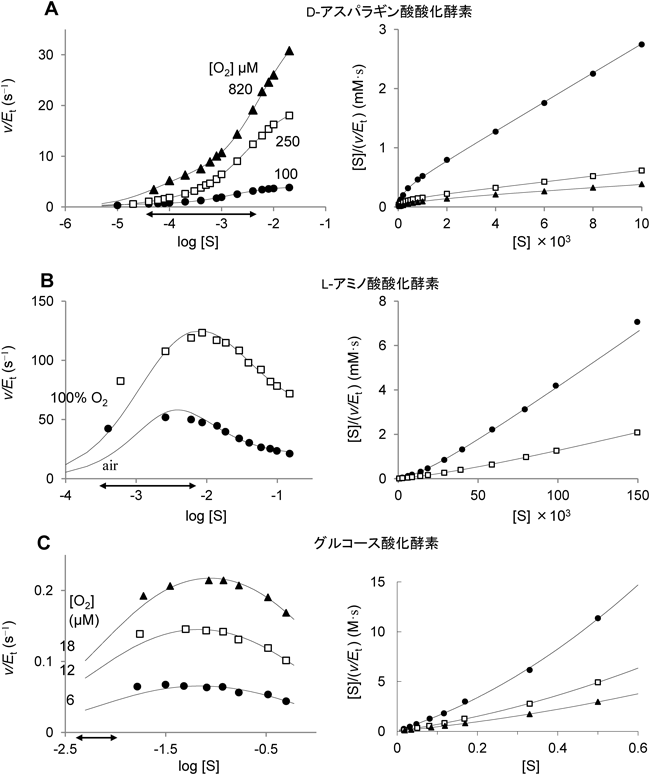
遊離型D-アミノ酸が自然界に広く存在し，さまざまな生理活性を示すことがわかってきたのは比較的最近である．筆者らもD-アミノ酸を分解する酵素に焦点を当て研究を進めている^2–8)．あるとき，筆者らは，ブタ腎臓からD-アスパラギン酸酸化酵素（DDO）を精製し，生理的基質のD-アスパラギン酸に対するk_catとK_Mの値を求めようとした²⁾．ところが，得られたデータをHanes–Woolfプロットしてみると上に凸の曲線が得られた（図2Aの右図参照，この図のデータは異なる酸素濃度で調べた筆者らの未発表データ）．同じような基質活性化がウシ腎臓DDO⁹⁾やタコのDDO¹⁰⁾でも認められている．興味深いことに，大腸菌のL-アスパラギン酸酸化酵素でも，L-アスパラギン酸による基質活性化が起こる¹¹⁾．

一方，蛇毒に大量に含まれていて古くから研究されているL-アミノ酸酸化酵素（LAO）は，非常に顕著な基質阻害を示すことが知れられている¹²⁾．このWellnerらの論文¹²⁾のL-ロイシンに対するデータを読み取って2通りの方法でプロットし直したものを図2Bに示す．

グルコース酸化酵素も研究歴が長い酵素で，血糖測定に利用されているだけでなく，最近，Klinmanのグループによって酸化半反応（図3参照）の反応機構について大きな進展がもたらされた¹³⁾．本酵素は，空気飽和の条件ではミカエリス・メンテンの式に従う．しかし，低い酸素濃度条件下では，グルコースによる基質阻害を受けることをNicolらが発見している¹⁴⁾（筆者らも追試して確かめている）．彼らの論文のデータを読み取って比較しやすいようにプロットし直したものが図2Cである．

図3 フラビン依存性酸化酵素の反応

この三つのどの場合も，酸素濃度が低いほどより低い濃度で基質による活性化や阻害が起こっていることに注目してほしい．DDOとLAOでは，生理的な基質濃度の変動範囲（図2中の両矢印）と活性化・阻害とが重なっている．しかし，基質濃度が生理的濃度より高いデータ（図2のHanes–Woolfプロットで近似的に直線が引ける部分）のみを使った解析しかなされておらず，筆者らが試みるまで²⁾ミカエリス・メンテンの式に代わる速度式を明示したデータ解析は行われていない．

哺乳動物のD-アミノ酸酸化酵素（DAO）は，LAOよりも早くから研究されてきたフラビン酵素である¹⁵⁾．両者は異なる祖先タンパク質から進化してきた酵素群であるが，DAOでは基質阻害や活性化の報告例はほとんどない．基質とするアミノ酸がL型であるかD型であるかを別にすれば，反応機構は基本的に同じであると考えられている．最近のRhodococcus opacus由来LAOの結晶構造解析の結果もそのことを示唆している¹⁶⁾．そうであるのに，なぜ一方は基質阻害・活性化を示し，他方は示さないのか．もし適応的な進化が関係しているとすれば，基質阻害・活性化が生理的な意味を持つ可能性がある．

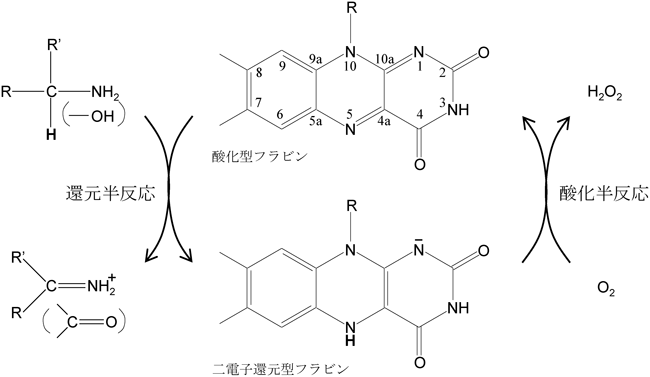
フラビン依存性酸化酵素の触媒反応は，還元半反応と酸化半反応とから構成される（図3）．還元半反応では，基質から酸化型フラビンへ二電子の移動とN（5）へのα-プロトン（基質のアミノ基やヒドロキシ基が結合している炭素原子に結合している水素原子）の付加が起こり，基質は酸化され，フラビンはアニオン型の還元型フラビンになる．たとえば，基質がアミノ酸の場合は，対応する2-イミノ酸が生じる．

酸化半反応では，還元型のフラビンが酸素分子と反応して酸化され，酸化型フラビンに戻り，一方，酸素分子は二電子還元されて過酸化水素になる．

フラビンは可視部に強い吸収を示すので，フラビンを通して触媒サイクルの進行を追跡することができ，また，嫌気技術を使うことで，還元半反応を酸化半反応から分離して調べることができる．このような特徴から，このフラビン酵素群では非常に精密な研究が展開されている．

酸素分子は気体であり，その溶解度は低く，100%酸素で反応液をバブリングしても1気圧での酸素濃度は1 mmol/Lを少し上回る程度にしかならない．また，水溶液中の拡散速度も遅いので，生体内部の生理的酸素濃度は空気飽和の約250 µmol/Lよりもかなり低いことを忘れてはならない．すなわち，少量の酸素分子しかない生体内では，酸化半反応がフラビン依存性酸化酵素の触媒サイクルを律速する可能性が高くなる．

酸化半反応の速度を考えるとき，酸素分子の基底状態が不対電子を2個持つ三重項状態であるのに対し，還元型フラビンは不対電子を持たない一重項状態であることも重要なポイントである．この結果，還元型フラビンから最初の一電子が酸素に移動する段階が酸化半反応の律速段階になる¹⁷⁾．近年，電子移動反応の基礎理論であるマーカス理論に基づく酸化半反応の精密な研究が活発になっている^18,19)．

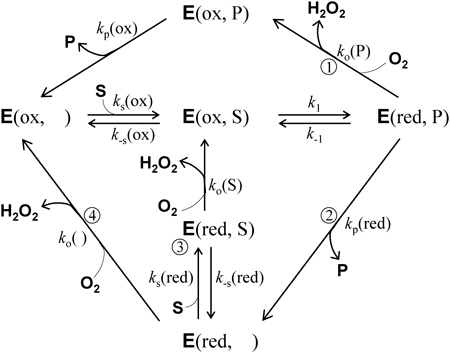
フラビン依存性酸化酵素の反応で，無視することができない反応中間状態だけを残した反応モデルを図4に示す．これと同じモデルは，堀池らがピリドキサミン（ピリドキシン）5′-リン酸酸化酵素の基質阻害を説明するために²⁰⁾，また，Ramsayがモノアミン酸化酵素AとBの反応機構を統一的に解釈するために²¹⁾，それぞれ提案している．しかし，この反応モデルに対して定常状態の近似により反応速度式を導き，その式に基づいて定量的にデータを論じた例は筆者の知る範囲ではない．

図4 フラビン依存性酸化酵素の反応モデル

括弧の中の左側の文字ox，redは，それぞれフラビン補酵素が酸化型，還元型であることを示す．右側の文字，S，Pは，それぞれ基質，生成物が結合していることを示し，空白は何も結合していないことを示す．

遊離型の酸化型酵素E(ox, )に基質Sが結合し，酸化型酵素基質複合体E(ox, S)ができる．この複合体の活性部位で基質から酸化型フラビンへ2個の電子とプロトンが転移し，還元型酵素生成物複合体E(red, P)が生じる（還元半反応）．E(red, P)は，二つの（図4の①と②）どちらかの経路をとる．一つは，生成物を放出する前に酸素と反応して酸化型酵素生成物複合体E(ox, P)となり（図4の①），E(ox, P)が生成物Pを放出してE(ox, )を再生する．D-アミノ酸酸化酵素のように，還元型酵素に対する生成物の結合が強く，しかも生成物が結合していることで還元型フラビンと酸素との反応性が高められる場合には，この経路が主要な反応経路になる．

E(red, P)がとる可能性がある二つめの経路（図4の②）では，酸素と反応する前にPを放出して遊離型の還元型酵素E(red, )ができる．このE(red, )には，二つの可能な経路がある（図4の③と④）．④の経路では，そのまま酸素と反応してE(ox, )を再生する．③の経路では，酸素と反応する前に基質Sを結合して還元型酵素基質複合体E(red, S)を生じる．E(red, S)は，フラビンは還元型であるので基質を酸化する能力はなく，このままでは酵素反応に役立たない．しかし，酸素と反応してE(ox, S)に変化することができると，次の還元半反応が始まるので，E(red, S)は酵素反応に寄与する中間体の一つになることができる．

この酵素反応モデルの特徴を要約すると，以下の三つの反応経路（A, B, C）が共存して回転することである．

経路AとBでは，遊離型酸化型酵素E(ox, )から反応サイクルが始まるが，経路Cでは遊離型還元型酵素E(red, )から反応サイクルが始まる．

基質が酵素の活性部位で酸化されるE(ox, S)→E(red, P)の段階と，酵素から生成物が遊離する段階，E(red, P)→E(red, )とE(ox, P)→E(ox, )は，基質濃度や酸素濃度とは無関係の一次の反応である．

もしE(red, P)から生成物が離れられない（k_p(red)=0）場合は，反応サイクルは経路Aのみとなり，酵素反応はミカエリス・メンテンの式に従う．したがって，基質活性化や阻害を示す酸化酵素は，必ずk_o(P)[O₂]と比べて無視できないだけの大きさのk_p(red)を示す，すなわちE(red, P)から生成物が遊離しやすい性質を持たなければならない．

図4に示した反応モデルから，定常状態の近似により得られる速度式を図5に示す（図5の式E1，k_p(red)>0）．式E1は四つのパラメータ（a₀, a₁, a₂, C₀）を持つ．式E2は式E1から導かれるHanes–Woolfプロットに対応した式で，この式では線形パラメータが三つ（a₀, a₁, a₂），非線形パラメータが一つ（C₀）となり，非線形最小二乗法によるデータ解析が容易になる．実際，図2の曲線は実験データを式E2に当てはめて求めた理論曲線で，実験データの示す関係をかなりよく再現できている（ただし，論文から採用した図2Bと2Cのデータは，低濃度側のデータポイント不足のため，収束はしなかった）．

図5 フラビン依存性酸化酵素の速度式

さて，式E3でk_o( )をゼロとすると，パラメータC₀がゼロになる．このとき，式E4から，パラメータa₀もゼロとなり，式E1は，以下のようにミカエリス・メンテン型の速度式になる．$$\begin{array}{}\text{(2)}& v=\frac{a_2^{-1}{E}_1\left[\text{S}\right]}{a_1{a}_2^{-1}+\left[\text{S}\right]}\end{array}$$したがって，基質活性化・阻害が起こるためには，前節でわかったk_p(red)>0の条件に加え，k_o( )>0の条件，すなわち，遊離型還元型酵素E(red, )が酸素と反応して酸化型酵素E(ox, )に戻ることが可能でなければならない．

パラメータC₀は，ミカエリス定数と同様に，濃度の単位を持つ．C₀はどのような濃度を意味するのか．E(red, )がE(red, )→E(red, S)→E(ox, S)（図4の経路③）とE(red, )→E(ox, )（図4の経路④）の二つのルートのうち，前者のルートを取る確率Qを求めてみる．Qは，E(red, S)→E(ox, S)の反応速度k_o(S)[O₂][E(red, S)]と，E(red, )→E(ox, )の反応速度k_o( )[O₂][E(red, )]との和に対する前者の速度の比になる（[X]でXのモル濃度を示す）．定常状態なので，[E(red, S)]と[E(red, )]には以下の関係がある．$$\begin{array}{}\text{(3)}& \left(k_{\text{o}}(\text{S})\left[{\text{O}}_{\text{2}}\right]+k_{-\text{s}}(\text{red})\right)\left[\text{E}(\text{red},\text{S})\right]=k_{\text{s}}(\text{red})\left[\text{S}\right]\left[\text{E}(\text{red},)\right]\end{array}$$式3の関係を用いて比を計算し，式E3を用いると，確率Qは次式のように表される．$$\begin{array}{}\text{(4)}& Q=\frac{\left[\text{S}\right]}{C_0+\left[\text{S}\right]}\end{array}$$式4から，基質濃度がC₀に等しいとき，確率Qが0.5になることがわかる．つまり，基質濃度がC₀より低い間は経路④が優勢で，基質濃度がC₀に等しいとき経路③の速度が経路④の速度と等しくなり，C₀を超えてさらに基質濃度が高くなると経路③が優勢になる．C₀を境にして主となる反応経路が変わるので，C₀は基質活性化・阻害が表に出てくる基質濃度の目安になっている．

式E3から，酸素濃度が低いほど，また，還元型酵素と基質との結合が強いほど（解離定数K_ds(red)が小さいほど）C₀が小さくなることがわかる．酸素濃度が低いほど，より低い基質濃度で基質活性化・阻害が認められる（図2）のは，酸素濃度が低くなるほどC₀値が小さくなるからである．

式E1のパラメータa₂は時間の単位を持つ（図5）．式E1で基質濃度を大きくしていくと，初速度はE_t/a₂に漸近する．また，式E2から，C₀やa₀の値よりも基質濃度が十分高い濃度領域ではHanes–Woolfプロットが直線に近づくことがわかる．しかし，その直線を特徴づけるパラメータa₁やa₂は，速度定数の複雑な関数になっていて（図5），その上，酸素濃度も含まれており，簡単には解釈できない．

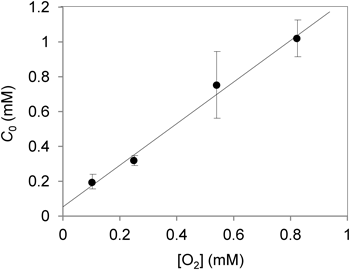
式E3（図5）は，いろいろな酸素濃度条件下で基質濃度を変えてkineticsを行い，得られたC₀値を酸素濃度に対してプロットすると直線が得られることを示している．その傾きから，遊離型の還元型酵素E(red, )が酸素分子と反応する2分子反応速度定数k_o( )と基質がE(red, )に結合する反応の速度定数k_s(red)と比を求めることができる．また，このプロットの縦軸切片は，E(red, )と酸素との反応速度k_o( )とE(red, S)と酸素との反応速度k_o(S)との比に還元型酵素と基質の結合に対する解離定数（K_d(red)）をかけたものになる．したがって，解離定数がわかっていれば，還元型酵素に基質が結合することで酸素との反応性がどれだけ変化するかを求めることができる．

ブタ腎臓D-アスパラギン酸酸化酵素（DDO）について，さまざまな酸素濃度下でD-アスパラギン酸の濃度を変えてkineticsを行い，得られたデータを式E2に当てはめてC₀値を求め，酸素濃度に対してプロットした結果を図6に示す（未発表データ）．一方で，嫌気チャンバーの中で還元型酵素を基質のD-アスパラギン酸で分光滴定し，微小であるが有意なスペクトル変化を利用して，解離定数K_d(red)を求めた．この値（2.3 mM）と図6のプロットの縦軸切片から，k_o(S)/k_o( )が39であることがわかった（未発表）．また，このプロットの傾きから，k_o( )/k_s(red)は1.2と求めることができた．DDOの場合，還元型酵素に基質が結合することで酸素との反応性が約40倍高くなること，還元型酵素が基質と結合して還元型酵素基質複合体を形成する反応の速度定数と酸素との反応の速度定数がほぼ等しいこと，この両方の性質により顕著な基質活性化が出現することが示唆された．

図6 パラメータC₀と酸素濃度との関係

ミカエリス・メンテンの式に従わない酵素反応では，触媒サイクル中に想定できるすべての反応中間体をまず考え，その中から取捨選択をし，できるだけ単純な反応モデルを作って速度式を導き，その特徴をじっくり考えることが大切である．定常状態のkineticsは，結晶構造解析や遷移状態の測定法や理論計算がいくら進歩しても，酵素研究の基礎であり，酵素の反応機構や生理的役割を解明する原点であることに変わりはない．酵素反応がミカエリス・メンテンの式に従わないと，とりあえずどうしていいかわからないし，非常に困惑する．無理に解釈しようとせずに，縦軸に初速度，横軸に基質濃度の常用対数をとって，データを記録することがまずは大切と思われる．筆者らも，実際のデータを図で示してくれている論文^11,12,14)に非常に助けられた．