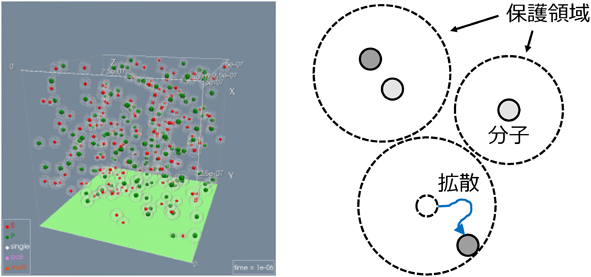
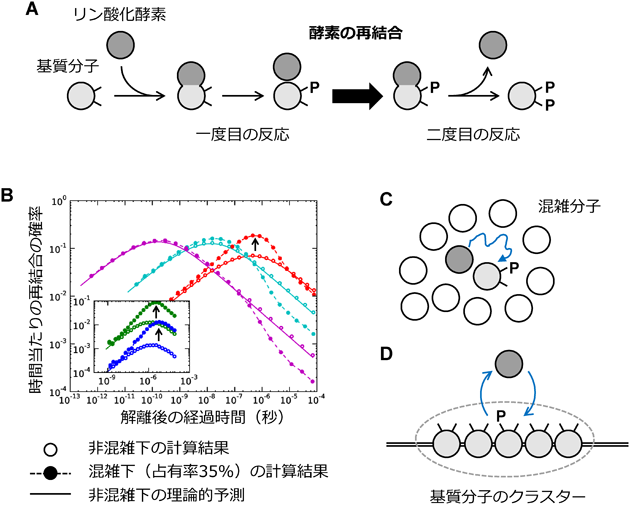
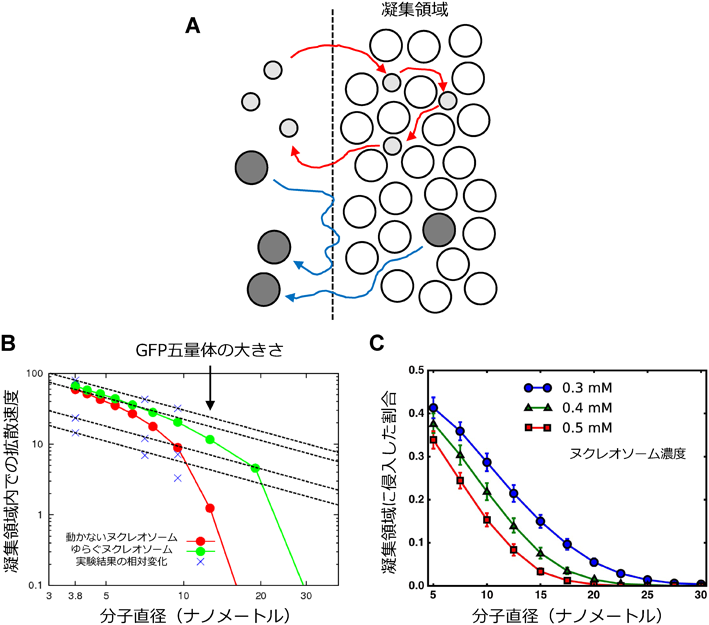
細胞環境下の生命システムを再現した1分子粒度シミュレーションBiochemical simulations at the molecular level reveal novel effects of cellular environments
国立研究開発法人理化学研究所生命システム研究センター生化学シミュレーション研究チームLaboratory for Biochemical Simulation, RIKEN Quantitative Biology Center (QBiC) ◇ 〒565–0874 大阪府吹田市古江台6–2–3 ◇ 6–2–3 Furuedai, Suita, Osaka 565–0874, Japan